SpaceCharge Class

The SpaceCharge class models the space charge forces in a particle beam by solving the Poisson equation in the bunch frame. Then the Lorentz transformed electromagnetic field is applied as a kick in the laboratory frame. For the solution of the Poisson equation we use an integral representation of the electrostatic potential by convolution of the free-space Green's function with the charge distribution. The convolution equation is solved with the help of the Fast Fourier Transform (FFT). The same algorithm for solution of the 3D Poisson equation is used, for example, in ASTRA.

Parameters:

• step (int): Step size used in unit steps. Default is 1.
• nmesh_xyz (list): Defines the number of mesh points in each dimension for the 3D mesh. Default is [63, 63, 63].
• low_order_kick (bool): Whether to use a low-order approximation for the kick. Default is True.
• random_mesh (bool): If True, the mesh is shifted slightly at each step to reduce numerical noise. Default is False.
• random_seed (int): Seed for random number generation when random_mesh is True. Default is 10.

Methods:

__init__(self, step=1, **kwargs)

Constructor to initialize the SpaceCharge class with the specified parameters. It sets up the mesh, the randomization flag, and the random seed.

prepare(self, lat)

Prepares the simulation by checking the step size and setting the random seed if necessary.

sym_kernel(self, ijk2, hxyz)

Computes the symmetric kernel for the 3D Poisson equation solution using the convolution method. The kernel is used to calculate the electrostatic potential in the beam.

potential(self, q, steps)

Solves the Poisson equation for the electrostatic potential in the beam, given the charge distribution (q) and step sizes (steps). This method uses the Fast Fourier Transform (FFT) for efficient computation.

el_field(self, X, Q, gamma, nxyz)

Calculates the electric field in the rest frame of the bunch by using a 3D interpolation method. The result is Lorentz transformed to the laboratory frame.

apply(self, p_array, zstep)

Applies the space charge kick to the particle array (p_array) over a given path length (zstep). The method computes the electric field and updates the particle momenta according to the space charge forces.

__repr__(self) -> str

Returns a string representation of the SpaceCharge class, including key parameters like step size, mesh resolution, and randomization settings.

---

Summary

The SpaceCharge class simulates the space charge forces acting on a particle beam by solving the Poisson equation for the beam's charge distribution. The class computes the electric field using a convolution method and applies the resulting forces as kicks to the particle array. This model is crucial for understanding beam dynamics, especially in high-intensity beams where space charge effects are significant.

---

Space Charge Example

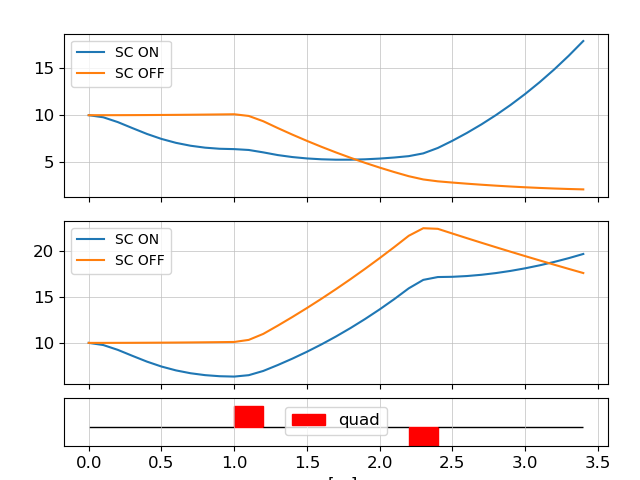
This example demonstrates how to simulate the impact of 3D space charge forces on the evolution of a particle beam through a simple FODO-like lattice. We compare tracking with and without space charge effects by plotting the resulting beta functions.

Step-by-Step

from ocelot import *
from ocelot.gui import *

# 1. Generate a test particle array with defined Twiss parameters
parray_init = generate_parray(
    nparticles=100000,
    tws=Twiss(beta_x=10, beta_y=10, E=0.01),  # E = 10 MeV
    sigma_tau=1e-4
)

# 2. Define a simple FODO-like lattice
qf = Quadrupole(l=0.2, k1=2)
qd = Quadrupole(l=0.2, k1=-2)
d = Drift(l=1)
m1 = Marker()  # Start of section
m2 = Marker()  # End of section

lat = MagneticLattice([m1, d, qf, d, qd, d, m2])

# 3. Tracking WITHOUT space charge
# Create navigator with step size 0.1 m
navi = Navigator(lat, unit_step=0.1)

# Add a dummy physics process to force tracking every step
emp = EmptyProc()
navi.add_physics_proc(emp, m1, m2)

parray = parray_init.copy()
tws_track_no_sc, _ = track(lat, parray, navi)

# 4. Tracking WITH 3D space charge
navi = Navigator(lat, unit_step=0.1)

# Create space charge process with default 3D mesh resolution
sc = SpaceCharge(nmesh_xyz=[63, 63, 63])
navi.add_physics_proc(sc, m1, m2)

parray = parray_init.copy()
tws_track_w_sc, _ = track(lat, parray, navi)

# 5. Plot beta functions with and without SC
fig, (ax_x, ax_y) = plot_API(lat, add_extra_subplot=True)

# Extract beta functions
s_no  = [tw.s for tw in tws_track_no_sc]
bx_no = [tw.beta_x for tw in tws_track_no_sc]
by_no = [tw.beta_y for tw in tws_track_no_sc]

s_sc  = [tw.s for tw in tws_track_w_sc]
bx_sc = [tw.beta_x for tw in tws_track_w_sc]
by_sc = [tw.beta_y for tw in tws_track_w_sc]

# Plot horizontal beta functions
ax_x.plot(s_no, bx_no, label="SC OFF")
ax_x.plot(s_sc, bx_sc, label="SC ON")
ax_x.set_ylabel(r"$\beta_x$ [m]")
ax_x.legend()

# Plot vertical beta functions
ax_y.plot(s_no, by_no, label="SC OFF")
ax_y.plot(s_sc, by_sc, label="SC ON")
ax_y.set_ylabel(r"$\beta_y$ [m]")
ax_y.set_xlabel("s [m]")
ax_y.legend()

plt.show()