This notebook was created by Mykola Veremchuk (mykola.veremchuk@xfel.eu), Svitozar Serkez. Source and license info is on GitHub. July 2019.

2. Reflection from imperfect highly polished mirror.

In this tutorial we will illustrate generation of imperfect surface and reflection of the radiation fields from it

from ocelot.optics.wave import * 
from ocelot.gui.dfl_plot import *

# setup logger level (it is not necessary)
from ocelot.optics.wave import _logger
import logging
_logger.setLevel(logging.ERROR)

from ocelot.gui.dfl_plot import _logger
_logger.setLevel(logging.ERROR)

    initializing ocelot...

# Activate interactive matplolib in notebook
import matplotlib
%matplotlib inline
# Setup figure white background 
matplotlib.rcParams["figure.facecolor"] = (1,1,1,1)
# Setup figure size
matplotlib.rcParams['figure.figsize'] = [10, 10]

Contents

1. Generating highly polished mirror
2. Reflection of radiation field from imperfect mirror

Highly polished mirror

Generation of mirror surfaces is based on W.Q. Hua, F.G. Bian, Y.M. He, W.H. Lin, L. Song, J. Wang, N. Zhao, Using the power spectral density method to characterize and evaluate the X-ray mirrors surfaces (2013)

We model mirror with 1D surface as the angle of incidence with respect to the surface is quite small in X-ray reflective optics.

The height errors along the axis

$$h^\prime (x) = \frac{M}{L} F^{-1} \Big( \sqrt{L \cdot PSD(k)} e^{j\phi(k)} \Big)$$

where

• $PSD(k)$ : power spectral density of the surface
• $M$ : number of points (pixels) on the surface
• $L$ : length of the surface
• $\phi(k)$ : randomly valued phase map ($-\pi < \phi(k) < \pi$)
• $k$ : wavevector

Reflection function is based on S. Serkez Design and Optimization of the Grating Monochromator for Soft X-Ray Self-Seeding FELs

PSD can be calculated using

$$PSD(k) = \frac{1}{L} \int_{-L/2}^{L/2} h(x) e^{-j2\pi kx} dx$$

PSD of a highly polished mirror typically yields a line in a loglog scale:

$$PSD(k) = b * k - \alpha$$

where

• $b$ is the slope of the power spectrum on a log-log scale
• $\alpha$ is determined by the fractal dimension D satisfying 1 < D < 2, D = (5 - $\alpha$) / 2

To generate HeightProfile with ocelot one can use the function:

hprofile = generate_1d_profile(hrms, length=0.1, points_number=1000)

• hrms: [m] height errors root mean square
• length: [m] length of the surface
• points_number: number of points of the surface

Optional parameters:

• wavevector_cutoff: [1/m] spacial frequency below which PSD(k) reaches plateou, default is 0
• psd: [m^3] 1d array; power spectral density of surface (if not specified, will be generated) (if specified, must have shape = (points_number // 2 + 1, ), otherwise it will be cut to appropriate shape)
• seed: seed for np.random.seed() to allow reproducibility

The function returns ocelot.optics.HeightProfile object, which can describe a geometry of not only the mirror surface

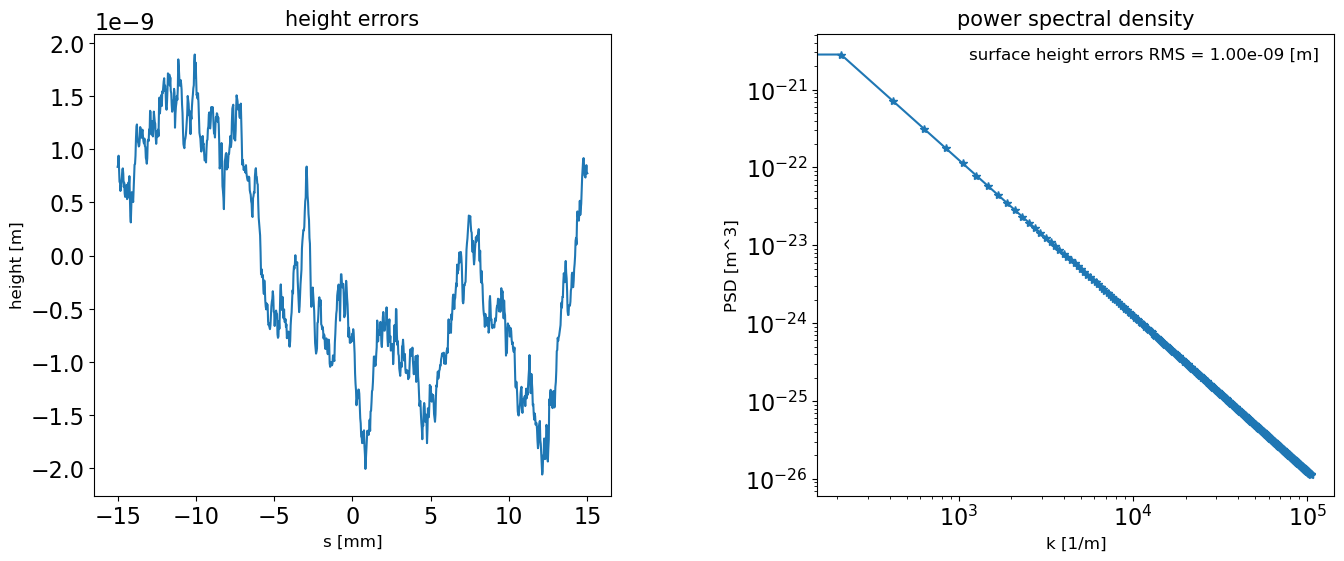
hprofile1 = generate_1d_profile(hrms=1e-9, length=0.03, points_number=1000, seed=666)

One can plot HeightProfile using function plot_1d_hprofile()

plot_1d_hprofile(hprofile1, fig_name='mirror1 height profile and PSD')

#HeightProfile with ```wavevector_cutoff = 10^3```
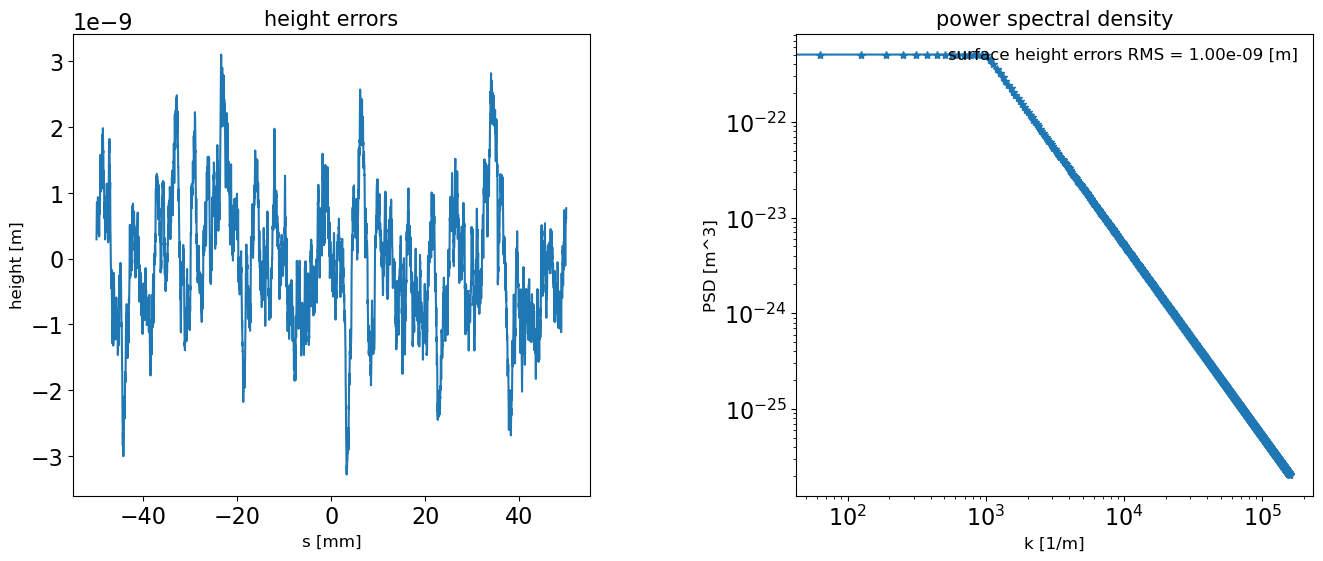
hprofile2 = generate_1d_profile(hrms=1e-9, length=0.1, points_number=5000, wavevector_cutoff=1e3)

plot_1d_hprofile(hprofile2, fig_name='mirror2 height profile and PSD')

Reflection radiation field from imperfect mirror

Reflection function implementation is discussed in S. Serkez, Design and Optimization of the Grating Monochromator for Soft X-Ray Self-Seeding FELs (2015), page 42-44 (see references therein).

A height error $\delta h$ on the optical surface will perturb the phase of a reflected wavefront $\delta \phi$

$$\delta \phi = \frac{4 \pi \delta h}{\lambda} \sin \theta_i$$

where

• $\theta_i$ : the radiation angle of incidence with respect to the mirror surface
• $\lambda$ : the radiation wavelength

To reflect radiation field (ocelot.optics.wave.RadiationField) off the mirror with height (ocelot.optics.wave.HeightProfile) there is the function:

dfl_reflect_surface(dfl, angle, height_profile=None, axis='x')

• dfl: RadiationField object from ocelot.optics.wave
• angle: [rad] angle of incidence with respect to the surface
• height_profile: HeightProfile object of the reflecting surface (if not specified, will be generated using hrms)
• axis: direction along which reflection takes place

Optional parameters:

• hrms: [m] height root mean square of reflecting surface (if height_profile is not specified, hrms will be used to generate height_profile internally)
• seed: seed for np.random.seed() to allow reproducibility
• return_height_profile: boolean type variable; if True, the function will return height_profile which was used for reflection

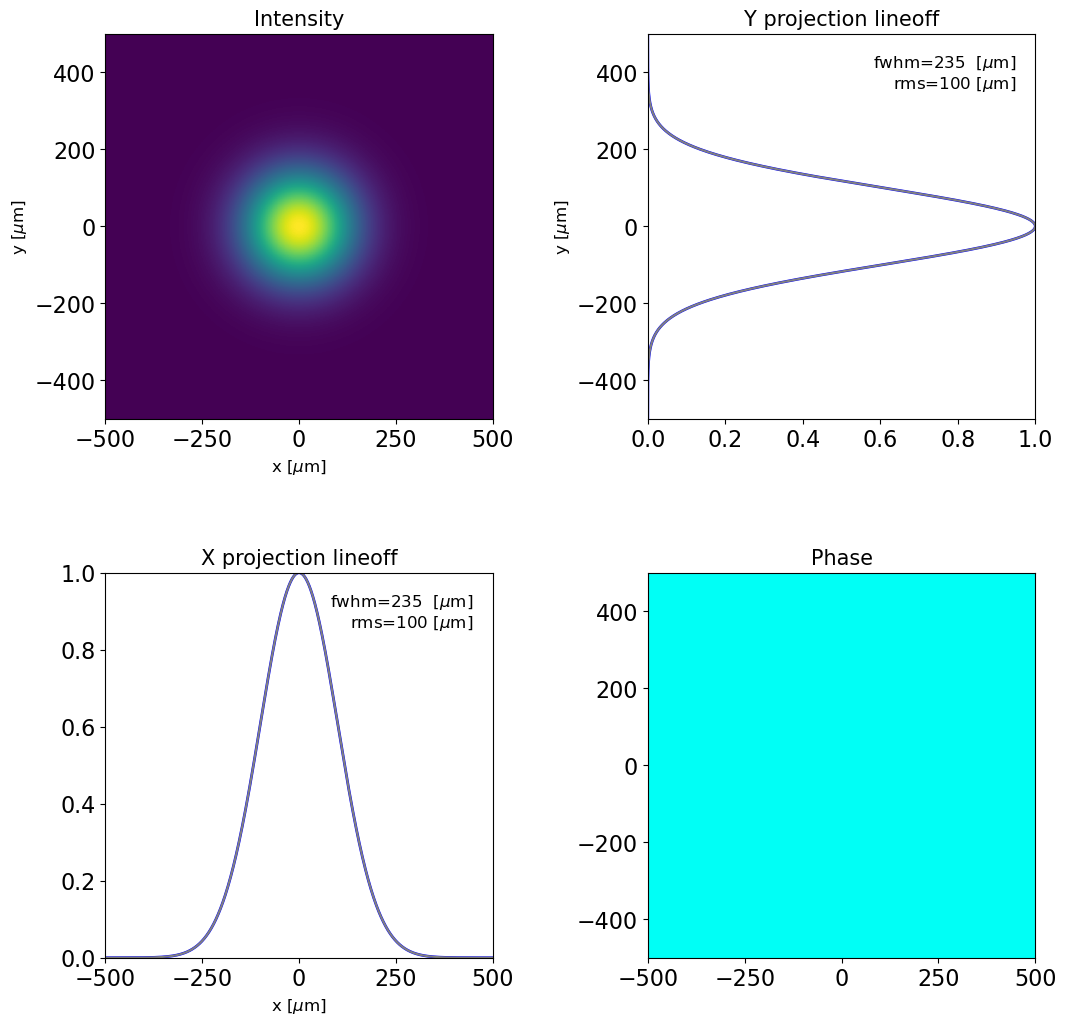
# generating gaussian RadiationField
dfl1 = generate_gaussian_dfl(1e-9, (1000, 1000, 1))

#radiation ritght before mirror1
plot_dfl(dfl1, phase=1, fig_name='radiation before the mirror1')

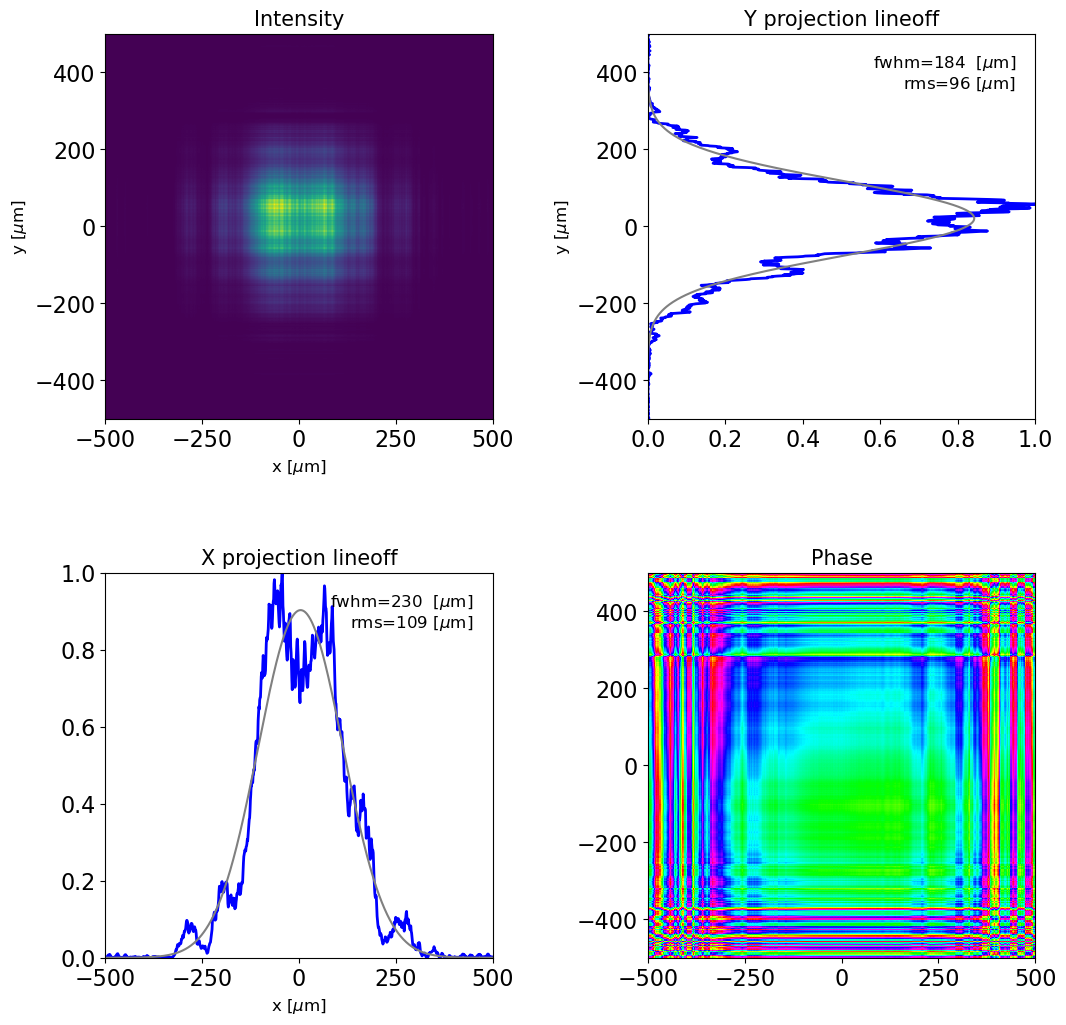
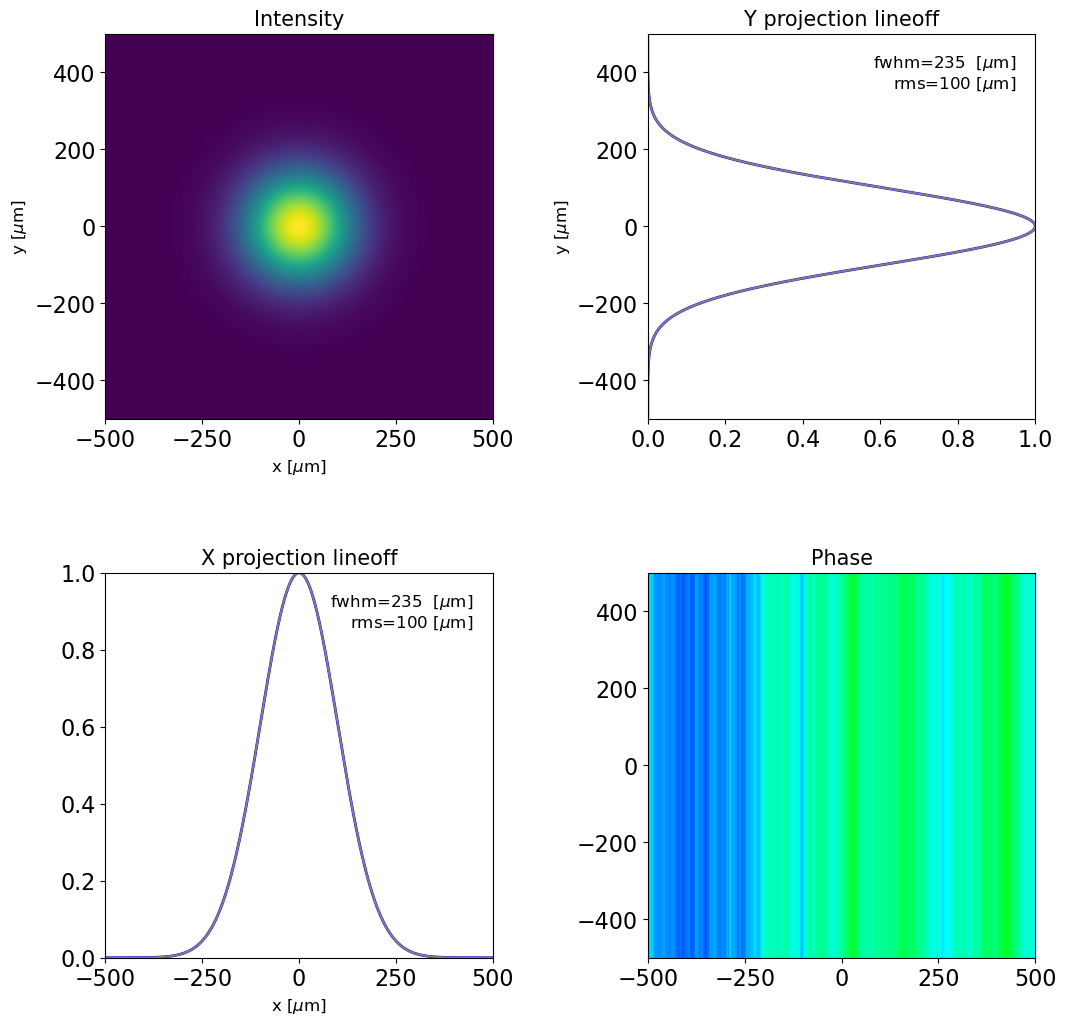
# reflecting RadiationField from mirror1 and plotting the result
dfl_reflect_surface(dfl1, angle=np.pi * 2 / 180, height_profile=hprofile1, axis='x')
plot_dfl(dfl1, phase=1, fig_name='radiation after reflection from mirror1')

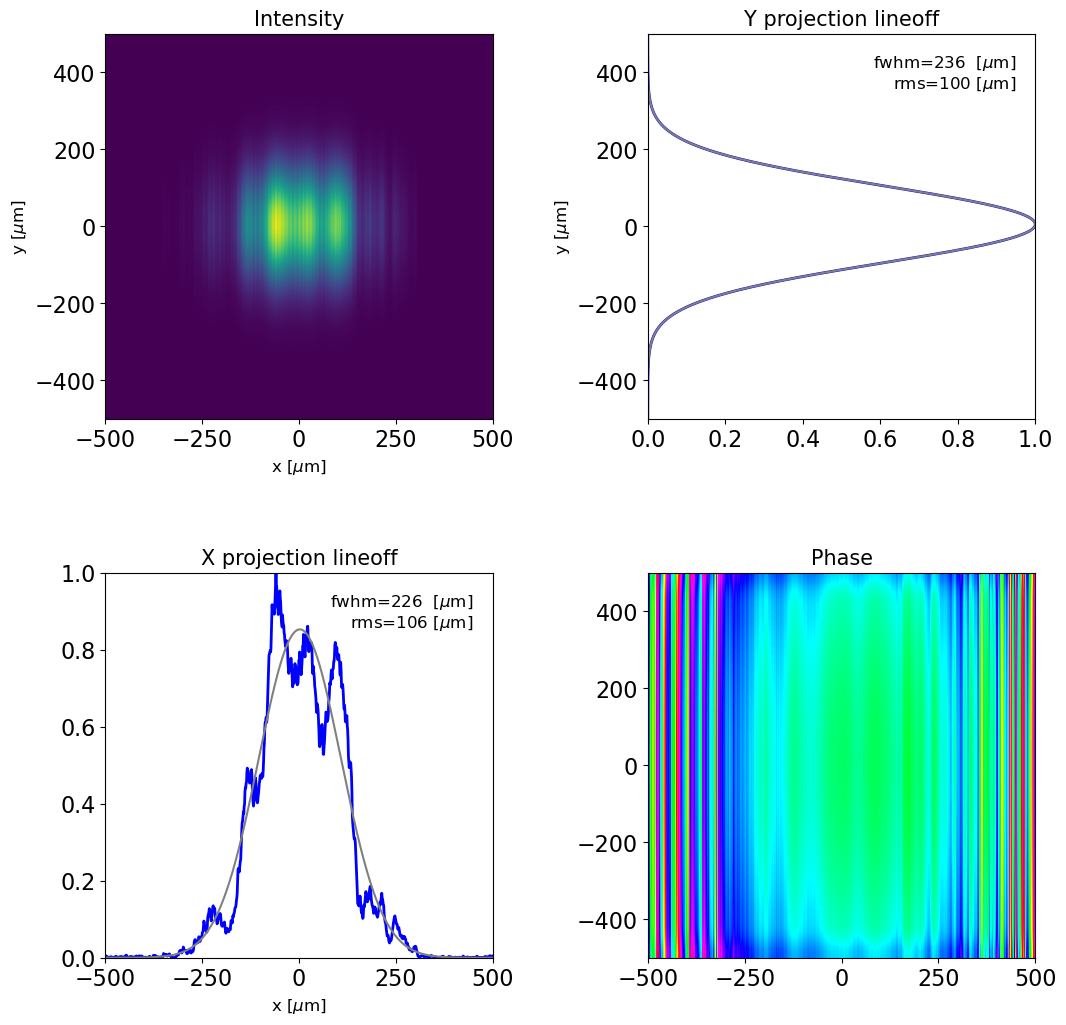
# propagating RadiationField after reflection for 10 meters and plotting the result
dfl1.prop(z=10)
plot_dfl(dfl1, phase=1, fig_name='radiation after reflection from mirror1 and propagation')

# reflecting RadiationField from another imperfect mirror vertically (also ```height_profile``` is not specified, so it will be generated internally)
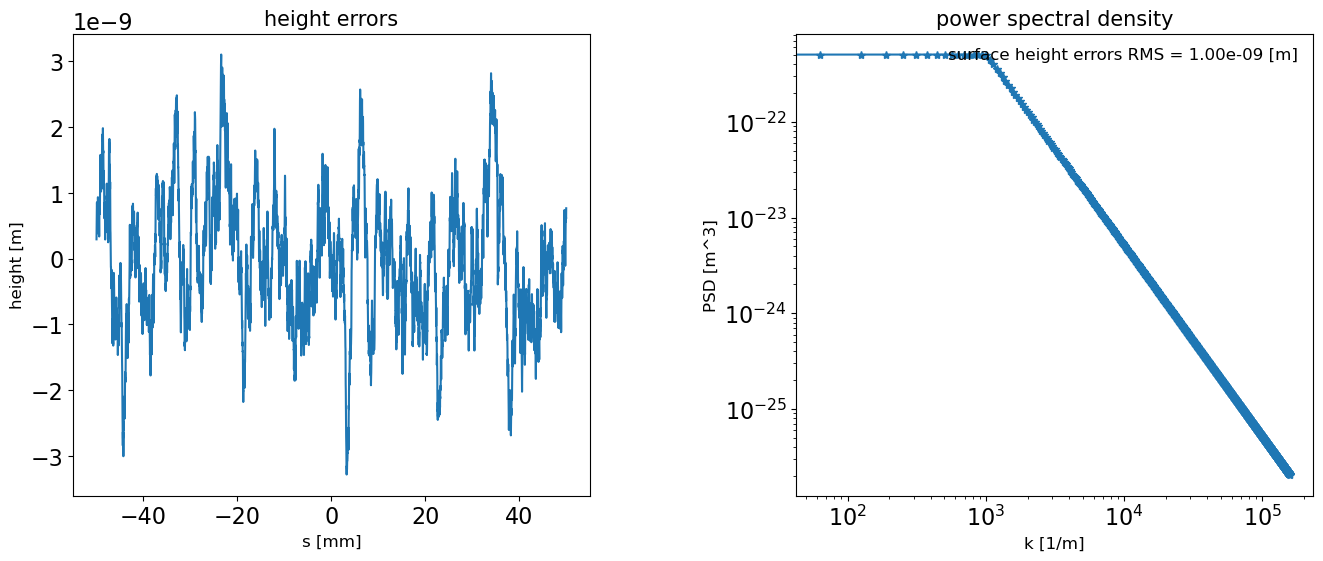
hprofile3 = dfl_reflect_surface(dfl1, angle=np.pi * 2 / 180, hrms=1e-9, axis='y', return_height_profile=1, seed=13)
plot_1d_hprofile(hprofile2, fig_name='internally generated mirror3 height profile and PSD') 
plot_dfl(dfl1, phase=1, fig_name='radiation after reflection from mirror3')

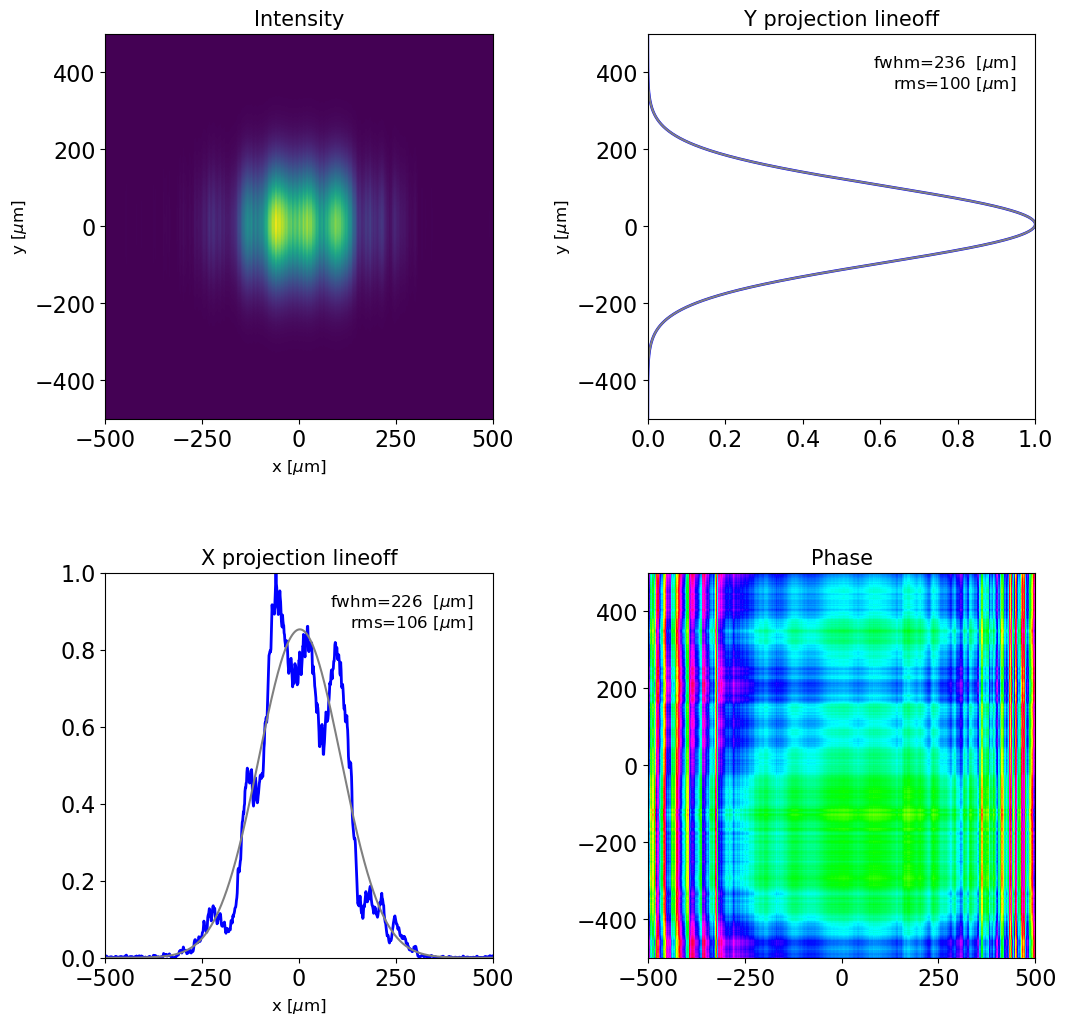
# propagating RadiationField for another 10 meters and plotting the result
dfl1.prop(z=10)
plot_dfl(dfl1, phase=1, fig_name='result of reflection from two rough mirrors')