This notebook was created by Sergey Tomin (sergey.tomin@desy.de). June 2018.

12. Undulator Matching

Appendix: FODO in thin lens approximation

This notebook was created as an answer for a question what the min/max average beta function can have the EuXFEL SASE1 undulator. The right way is asking the optics expert but it is too simple and does not make you feel the beam optics of this SASE line. Another problem is that FEL experts like to work with average betas. To meet all these requirements, I wrote this notebook, which also might help someone to understand how to deal with linear optics in OCELOT.

Let's consider the FODO cell of the SASE undulator

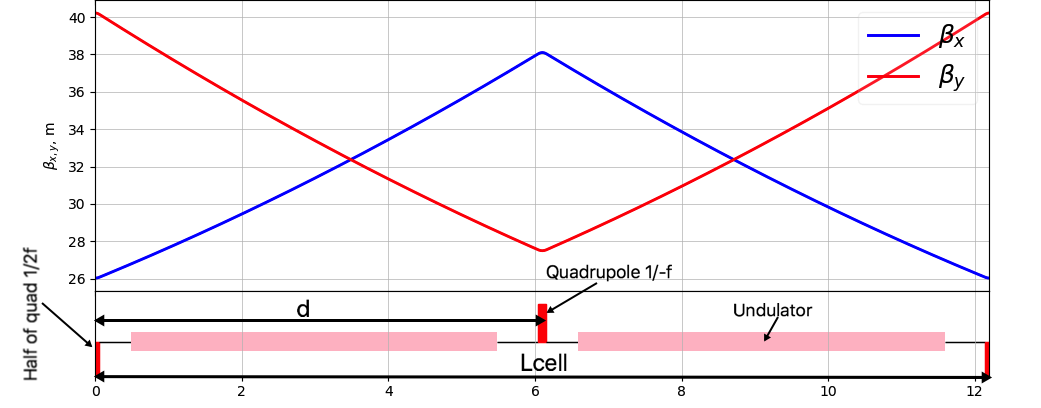
Introducing $d = L_{cell}/2$ as the distance between defocusing and focusing quadrupoles.

We neglect focusing effect in the vertical plan of the horizontal planar undulator.

The transfer matrix of the quadrupole in thin lens approximation:

$$M_f = \begin{bmatrix} 1 & 0 \\ 1/f & 1 \end{bmatrix}$$

where $f = 1/kl$ is focal length, $k$ is quad strength and $l$ is the quad length.

Drift:

$$M_d = \begin{bmatrix} 1 & d \\ 0 & 1 \end{bmatrix}$$

%matplotlib inline
import sympy as sp 
sp.init_printing()

Calculate the matrix for a half cell, starting in the middle of a defocusing quadrupole and ending in the meddile of a focusing lens.

And denotes $f_h = 2 f$ focal length of the half quadrupole

fh, d = sp.symbols("fh, d")

Mqf = sp.Matrix([[1, 0],[-1/fh, 1]])
Md = sp.Matrix([[1, d],[0, 1]])
Mqd = sp.Matrix([[1, 0],[1/fh, 1]])
M1 = Mqf*Md*Mqd
sp.simplify(M1)

$\displaystyle \left[\begin{matrix}\frac{d + fh}{fh} & d\\- \frac{d}{fh^{2}} & \frac{- d + fh}{fh}\end{matrix}\right]$

For second half cell $f_h \to -f_h$

M2 = sp.Matrix([
[(d - fh)/-fh,           d],
[    -d/fh**2, (-d -fh)/-fh]])
M_cell = sp.simplify(M1*M2)
M_cell

$\displaystyle \left[\begin{matrix}- \frac{2 d^{2}}{fh^{2}} + 1 & \frac{2 d \left(d + fh\right)}{fh}\\\frac{2 d \left(d - fh\right)}{fh^{3}} & - \frac{2 d^{2}}{fh^{2}} + 1\end{matrix}\right]$

Phase advance and stability of the FODO cell

Phase advance is related to the transfer matrix by:

$$\cos \phi_{cell} = \frac{1}{2}Trace(M_{cell})$$

Stability requares:

$$\left|Trace(M_{cell})\right| < 2$$

trace_M = sp.simplify(M_cell[0,0] + M_cell[1,1])
trace_M

$\displaystyle - \frac{4 d^{2}}{fh^{2}} + 2$

Phase advance:

$$\cos \phi_{cell} = \frac{1}{2}Trace(M_{cell}) = \frac{1}{2} \Big(2 - \frac{4 d^2}{f_h^2}\Big) = 1 - \frac{2 d^2}{f_h^2} = 1 - 2\frac{L_{cell}^2}{16 f^2}$$

using trigonometric double-angle formulae:

$$\cos 2\phi = 1-2\sin^2 \phi$$

and finally

$$\boxed{\sin \phi_{cell}/2 = \frac{L_{cell}}{4f}}$$

Stability

$$\left| 2 - \frac{4 d^2}{f_h^2}\right| < 2$$

rewriting

$$0 < \frac{4 d^2}{f_h^2} < 4 \qquad \to \qquad f_h > d$$

Finally

$$\boxed{f > \frac{L_{cell}}{4}}$$

$\beta$ - functions

General solution of the Hill's equation $x'' + K(s)x = 0$:

$$\begin{cases} x(s) = \sqrt{\varepsilon \beta(s)}\cos(\phi(s) + \phi)\\ x'(s) = -\sqrt{\frac{\varepsilon}{\beta(s)}}\Big(\alpha(s)\cos(\phi(s) + \phi) + \sin(\phi(s) + \phi)\Big) \end{cases}$$

Applying initial conditions at the point $s(0) = s_0$ with $\phi(0) = 0$ and the particle coordinates $x_0, x'_0$, we will get:

$$\begin{cases} \cos\phi = \frac{x_0}{\sqrt{\varepsilon \beta_0}}\\ \sin\phi = -\frac{1}{\sqrt{\varepsilon}}\Big( \frac{\alpha_0}{\sqrt{\beta_0}}x_0 + \sqrt{\beta_0}x'_0\Big) \end{cases}$$

inserting the result into the equation above:

$$\begin{bmatrix} x_1 \\ x'_1 \end{bmatrix} = \begin{bmatrix} \sqrt{\frac{\beta_1}{\beta_0}}(\cos\phi_{0\to1} + \alpha_0\sin\phi_{0\to1}) & \sqrt{\beta_1\beta_0}\sin\phi_{0\to1})\\ \frac{(\alpha_0 - \alpha_1)\cos\phi_{0\to1} - (1 + \alpha_0\alpha_2)\sin\phi_{0\to1}}{\sqrt{\beta_1\beta_0}} & \sqrt{\frac{\beta_0}{\beta_1}}(\cos\phi_{0\to1} - \alpha_1\sin\phi_{0\to1}) \end{bmatrix} \cdot \begin{bmatrix} x_0 \\ x'_0 \end{bmatrix}$$

Now consider half of the FODO cell (see picture above) ($\phi_{0\to1} = \phi_{cell}/2$) and $\beta_0 = \beta_{min}$ and $\beta_1 = \beta_{max}$ (we consider horizontal plane) and remembering that in the middle of the quads $\alpha = 0$. From another side, we have already calculated the transfer matrix for a half of FODO cell. Collecting all together:

$$\begin{bmatrix} \sqrt{\frac{\beta_{max}}{\beta_{min}}}\cos\frac{\phi_{cell}}{2} & \sqrt{\beta_{max}\beta_{min}}\sin\frac{\phi_{cell}}{2}\\ -\frac{\sin\frac{\phi_{cell}}{2}}{\sqrt{\beta_{max}\beta_{min}}} & \sqrt{\frac{\beta_{min}}{\beta_{max}}}\cos\frac{\phi_{cell}}{2} \end{bmatrix}; \qquad \begin{bmatrix} 1 + d/f_h & d \\ -d/f_h^2 & 1 - d/f_h \end{bmatrix}$$

after some gymnastics with trigonometric identities (and taking into account $\sin \phi_{cell}/2 = \frac{d}{f_h}= \frac{L_{cell}}{4f}$)

$$\beta_{max} = \frac{1 + \sin \frac{\phi_{cell}}{2}}{\sin\phi_{cell}}L_{cell}$$ $$\beta_{min} = \frac{1 - \sin \frac{\phi_{cell}}{2}}{\sin\phi_{cell}}L_{cell}$$

If we neglect the fact the beta function in the drift space takes the form of a quadratic function ($\beta(s) = \beta_0 - 2\alpha_0 s + \gamma_0 s^2$) and assume instead a linear behavior, the average $\beta$-function will be

$$\overline \beta \approx \frac{\beta_{max} + \beta_{min}}{2} = \frac{L_{cell}}{\sin\phi_{cell}}$$

What means that minimum average beta-function will be with phase advance $\phi_{cell} = 90^0$. For SASE1 undulator $L_{cell} = 12.2$ and taking into account that our calculations were done with some level approximation:

$$\overline \beta_{min} \approx \frac{12.2 m}{\sin 90^0} = 12.2 m$$

More accurate solution

Taking into account quadratic shape of the $\beta$ in the drift space and go through some simple steps, finally we will get more exact solution:

1. Twiss parameters transformation

$$\begin{bmatrix} \beta \\ \alpha \\ \gamma \end{bmatrix}_1 = \begin{bmatrix} C^2 & -2SC & S^2\\ -C C' & SC' + S'C & -SS'\\ C'^2 & -2 S'C' & S'^2 \end{bmatrix} \cdot \begin{bmatrix} \beta \\ \alpha \\ \gamma \end{bmatrix}_0$$

Where $C,S, C', S'$ are elements of the transfer matrix

$$M = \begin{bmatrix} C & S \\ C' & S' \end{bmatrix}$$

2. twiss parameters after the thin quadrupole:

$$\beta_1 = \beta_0 \\ \alpha_1 = -\frac{\beta_0}{f} + \alpha_0 \\ \gamma_1 = \frac{1}{f^2} - 2 \frac{\alpha_0}{f} + \gamma_0$$

In the middle of the quadrupole $\alpha_0 = 0$ then

$$\alpha_1 = -\frac{\beta_0}{f_h}$$

3. In the drift space $\beta$ behave:

$$\beta(s) = \beta_0 - 2\alpha_0 s + \gamma_0 s^2$$

4. Because FODO cell is symetric and we are considering the thin lens approximation the average $\overline \beta$ is:

$$\overline \beta = \frac{2}{L}\int_0^{L/2}\left(\beta_0 - 2\alpha_0 s + \gamma_0s^2 \right)ds = \beta_0 - \frac{\alpha_0 L}{2} + \gamma_0\frac{L^2}{12}$$

5. Inserting expression for $\beta_{min}$ and express focal length against the phase advance we will get:

$$\boxed{\overline \beta = \frac{L}{6 \sin\phi_{cell}}\big(5 + \cos\phi_{cell} \big)}$$

info

The result looks simple, probably this expression can be found in some handbooks.

The minimum possible average $\overline\beta_{min}$ will be with $\frac{d \overline \beta}{d\phi_{cell}} = 0$ what gives us $\phi_{cell} = \pi - \arctan 2\sqrt 6 \approx 101^0$.

And for our case $L_{cell} = 12.2 m$ it will be

$$\overline \beta_{min} \approx 9.96$$

Might be useful to find condition for minimum possible $\beta_{max}$

$$\frac{d}{d\phi}\beta_{max} = 0$$

phi = sp.Symbol("phi")
sp.diff((1 + sp.sin(phi/2))/sp.sin(phi), phi)

$\displaystyle - \frac{\left(\sin{\left(\frac{\phi}{2} \right)} + 1\right) \cos{\left(\phi \right)}}{\sin^{2}{\left(\phi \right)}} + \frac{\cos{\left(\frac{\phi}{2} \right)}}{2 \sin{\left(\phi \right)}}$

import numpy as np
from scipy.optimize import root
from matplotlib import pyplot as plt
fun = lambda phi: -(np.sin(phi/2) + 1)*np.cos(phi)/np.sin(phi)**2 + np.cos(phi/2)/(2*np.sin(phi))
res = root(fun, 0.1)
print("Cell phase advance for minimum possible bmax: phi = ", res.x*180/np.pi)

    Cell phase advance for minimum possible bmax: phi =  [76.34541525]

SASE1 undulator. Numerical simulation

%matplotlib inline
from ocelot import *
from ocelot.gui.accelerator import *
from scipy.integrate import simps
from ocelot.cpbd import optics

d1 = Drift(l=0.43065, eid='d1')
d2 = Drift(l=0.55565, eid='d2')
l = 0.1137
k = 2*0.1137/l

qd = Quadrupole(l=l/2, k1=-k, tilt=0.0)
qf = Quadrupole(l=l, k1=k, tilt=0.0)
K = 3
u40 = Undulator(lperiod=0.04, nperiods=125, Kx=K, Ky=0.0)
m1 = Marker()
m2 = Marker()
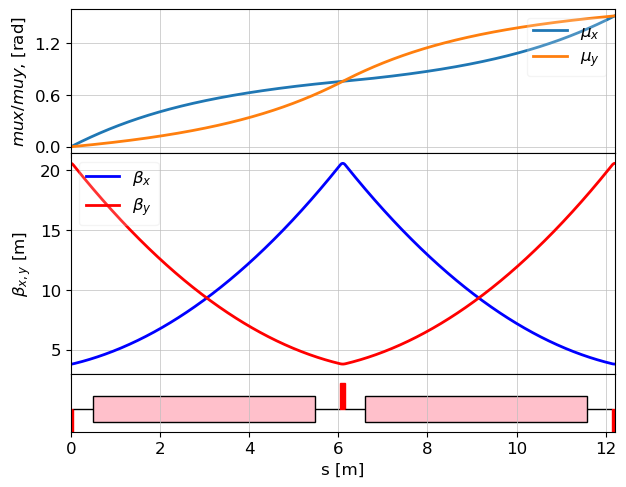
fodo_cell = [m1, qd, d1, u40, d2, qf, d1, u40, d2, qd, m2]
fodo_lat = MagneticLattice(fodo_cell)

tws = twiss(fodo_lat, nPoints=1000)

plot_opt_func(fodo_lat, tws, top_plot=["mux", "muy"], legend=False)
plt.show()

    initializing ocelot...

def beta(k):
    qd.k1 = -k
    qf.k1 = k
    fodo_lat.update_transfer_maps()
    tws = twiss(fodo_lat, nPoints=1000)
    bx = np.array([tw.beta_x for tw in tws])
    s = np.array([tw.s for tw in tws])
    bx_av = simps(bx, s)/fodo_lat.totalLen
    phi = tws[-1].mux
    L = fodo_lat.totalLen
    bx_av_th = L/6 * (5 + np.cos(phi))/np.sin(phi)
    return bx_av, bx.max(), bx.min(), tws[-1].mux*180/np.pi, bx_av_th

k = np.arange(0.3, 2.9, 0.05)
Bx_min = []
Bx_max = []
Bx_av = []
Bx_av_theory = []
Phi = []
for k1 in k:
    bx_av, bx_max, bx_min, phi, bx_av_th = beta(k1)
    Bx_min.append(bx_min)
    Bx_max.append(bx_max)
    Bx_av.append(bx_av)
    Phi.append(phi)
    Bx_av_theory.append(bx_av_th)
    
fig, ax1 = plt.subplots()
plt.title(r"$\beta$ - average and max against quad strength")
ax1.plot(k, Bx_av, label=r"$\beta_{av}$")
ax1.plot(k, Bx_av_theory,"g--", label=r"$\beta_{av}^{theory}$")
ax1.plot(k, Bx_max, label=r"$\beta_{max}$")
ax1.set_ylabel(r"$\beta$, m")
ax1.set_xlabel("k, 1/m2")
plt.legend()
print("min(beta_av) = ", np.min(Bx_av), "m" )
ax2 = ax1.twinx()
ax2.plot(k, Phi, "r", label=r"$\phi_{cell}$")
ax2.set_ylabel(r"$\phi_{cell}$", color='r')
ax2.tick_params('y', colors='r')
plt.legend()
plt.grid(False)
plt.show()

    min(beta_av) =  9.991835898036324 m

Limitations

The maximum possible strength of the undulator quadrupoles is $k_{max} = 1.94729$ what means that we can have minimum average beta-function close to 10m (see the Figure above).

Now we need to consider the limitations of the matching sections.

Inverse the task

Find the quad strength and FODO cell params if beta average is defined

FODO estimator

from scipy.optimize import root

def fodo_estimator(beta_av, Lcell, lq=0.1137):
    fun = lambda phi: Lcell/6 * (5 + np.cos(phi))/np.sin(phi) - beta_av
    res = root(fun, 0.1)
    phi = res.x[0]
    b_av = Lcell/6 * (5 + np.cos(phi))/np.sin(phi)
    f = Lcell/(4*np.sin(phi/2))
    kq = 1/f/lq
    bmax = (1 + np.sin(phi/2))/np.sin(phi)*Lcell
    bmin = (1 - np.sin(phi/2))/np.sin(phi)*Lcell
    return kq, phi, bmin, bmax, b_av
    
kq, phi, bmin, bmax, b_av = fodo_estimator(beta_av=11, Lcell=12.2)
print("k1 = ", kq, "1/m^2")
print("bmin / bmax = ", bmin, "/", bmax, "m")
print("calculated beta_av = ", b_av, "m")
print("phi = ", phi*180/np.pi, "deg")

    k1 =  1.771751963648942 1/m^2
    bmin / bmax =  4.851965262428619 / 20.314939511625177 m
    calculated beta_av =  11.000000000000059 m
    phi =  75.8191420392388 deg

FODO correction due to undulator focusing

def fodo_correction_SASE1(beta_av=60, K=3):
    kq, phi, bmin, bmax, b_av = fodo_estimator(beta_av=beta_av, Lcell=12.2)
    
    print("Estimation: beta_x = ", np.round(bmin,3), "; beta_y = ", np.round(bmax, 3),
          "; phi = ", np.round(phi*180/np.pi), "grad"
          "; kf/kd = ", np.round(kq, 4),"/", np.round(-kq, 4))
    
    # SASE1 FODO cell
    d1 = Drift(l=0.43065, eid='d1')
    d2 = Drift(l=0.55565, eid='d2')
    qd = Quadrupole(l=0.1137/2, k1=-kq, tilt=0.0)
    qf = Quadrupole(l=0.1137, k1=kq, tilt=0.0)
    u40 = Undulator(lperiod=0.04, nperiods=125, Kx=K, Ky=0.0)
    m1 = Marker()
    m2 = Marker()
    fodo_cell = [m1, qd, d1, u40, d2, qf, d1, u40, d2, qd, m2]
    
    # constraints
    constr = {fodo_cell[-1]: {'mux':phi, "muy":phi}, "periodic": True}

    # variables
    vars = [qf, qd]
    
    tws = Twiss()
    tws.beta_x = bmin
    tws.beta_y = bmax
    tws.E = 14
    
    res = match(MagneticLattice(fodo_cell), constr=constr,tw=tws, 
                vars=vars, max_iter=2000, verbose=False)
    kf, kd = res
    
    qf.k1 = kf
    qd.k1 = kd
    
    fodo_lat = MagneticLattice(fodo_cell)

    tws = twiss(fodo_lat, tws0=tws, nPoints=1000)
    print("Correction: beta_x = ", np.round(tws[0].beta_x, 3), 
          "beta_y = ", np.round(tws[0].beta_y, 3), 
          " kf/kd = ", np.round(kf,4), "/", np.round(kd,4))
    #plot_opt_func(fodo_lat, tws, top_plot=["mux", "muy"], legend=False)
    #plt.show()
    return kf, kd, bmin, bmax

Current lattice $\overline\beta \approx 32$ m

import sase1_lattice as sase1

lat = MagneticLattice(sase1.cell)#, stop=sase1.fodo_match)
print(sase1.tws)
#sase1.tws.beta_x = 15
#sase1.tws.beta_y = 50
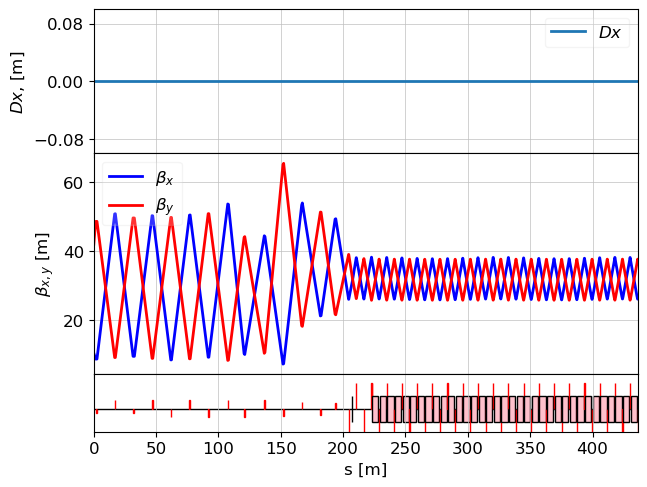
tws = twiss(lat, tws0=sase1.tws)
plot_opt_func(lat, tws, legend=False)
plt.show()

    emit_x  = 0.0
    emit_y  = 0.0
    beta_x  = 10.506745988156398
    beta_y  = 42.02704133328497
    alpha_x = 0.676085898798978
    alpha_y = -2.1449229692237783
    gamma_x = 0.0
    gamma_y = 0.0
    Dx      = 0.0
    Dy      = 0.0
    Dxp     = 0.0
    Dyp     = 0.0
    mux     = 0.0
    muy     = 0.0
    nu_x    = 0.0
    nu_y    = 0.0
    E       = 14
    s        = 0.0
    

$\overline \beta = 60$ m

Sometimes require run this cell two times to get a correct result

kf, kd, bmin, bmax = fodo_correction_SASE1(beta_av=60, K=3)
# constraints
constr = {sase1.fodo_match: {'beta_x':bmax, "beta_y":bmin, 
                             "alpha_x": 0, "alpha_y": 0}}

quad_limits = {sase1.qf_2177_t2: [-0.654, 0],
             sase1.qf_2192_t2: [0 ,0.654],
             sase1.qf_2207_t2: [-0.654, 0],
             sase1.qf_2218_t2: [0 ,0.654],
             sase1.qa_2229_t2: [-1.94, 0],
             sase1.qa_2235_t2: [0, 1.94]}
# variables
vars = [sase1.qf_2177_t2, sase1.qf_2192_t2,
        sase1.qf_2207_t2, 
        sase1.qf_2218_t2, sase1.qa_2229_t2, sase1.qa_2235_t2]

# because of variables redundancy, we can help a bit to find a more elegant solution 
# *** comment lines or change inital conditions if you want to play with matching
sase1.qf_2177_t2.k1 = -0.2244
sase1.qf_2192_t2.k1 = 0.2309
sase1.qf_2207_t2.k1 = -0.1911
sase1.qf_2218_t2.k1 = 0.1653
sase1.qa_2229_t2.k1 = -0.0881
sase1.qa_2235_t2.k1 = 0.0953

# *** comment lines or change inital conditions if you want to play with matching
lat.update_transfer_maps()

res = match(lat, constr=constr, vars=vars, tw=sase1.tws, max_iter=2000, verbose=False)

sase1.qa_2241_sa1.k1 = kd
sase1.qa_2247_sa1.k1 = kf
sase1.qa_2247_sa1_h.k1 = kf
lat.update_transfer_maps()
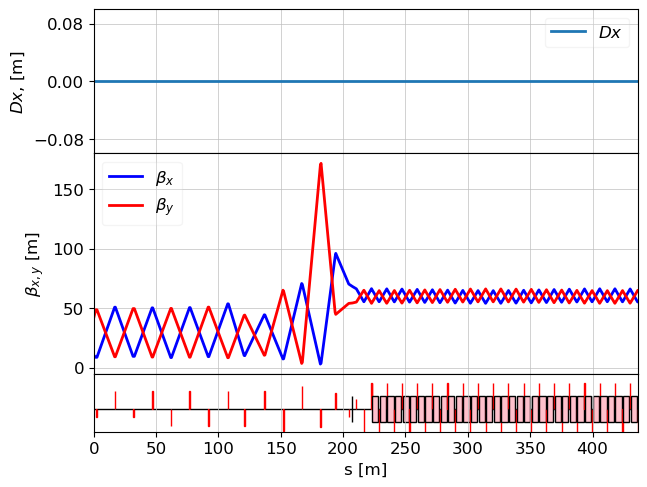
tws = twiss(lat, tws0=sase1.tws)
plot_opt_func(lat, tws, legend=False)
plt.show()

    Estimation: beta_x =  54.076 ; beta_y =  66.34 ; phi =  12.0 grad; kf/kd =  0.2937 / -0.2937
    initial value: x =  [0.29368260023214693, -0.29368260023214693]
    Optimization terminated successfully.
             Current function value: 0.000032
             Iterations: 40
             Function evaluations: 79
    Correction: beta_x =  54.076 beta_y =  66.34  kf/kd =  0.2648 / -0.2583
    initial value: x =  [-0.2244, 0.2309, -0.1911, 0.1653, -0.0881, 0.0953]
    Optimization terminated successfully.
             Current function value: 0.000031
             Iterations: 158
             Function evaluations: 279

Checking quads limits

# check quads limits
for q, k in zip(vars, res):
    print(q.id + ".k1 = "+ str(np.round(k,4)) +  ";   strength is OK :",
          quad_limits[q][0]<k<quad_limits[q][1])

    QF.2177.T2.k1 = -0.2244;   strength is OK : True
    QF.2192.T2.k1 = 0.2309;   strength is OK : True
    QF.2207.T2.k1 = -0.1911;   strength is OK : True
    QF.2218.T2.k1 = 0.1653;   strength is OK : True
    QA.2229.T2.k1 = -0.0881;   strength is OK : True
    QA.2235.T2.k1 = 0.0953;   strength is OK : True

$\overline \beta = 11$ m

Sometimes require run this cell two times to get a correct result

kf, kd, bmin, bmax = fodo_correction_SASE1(beta_av=11, K=3)
# constraints
constr = {sase1.fodo_match: {'beta_x':bmax, "beta_y":bmin, 
                             "alpha_x": 0, "alpha_y": 0}}


# variables
vars = [sase1.qf_2177_t2, sase1.qf_2192_t2, sase1.qf_2207_t2, 
        sase1.qf_2218_t2, sase1.qa_2229_t2, sase1.qa_2235_t2]

# because of variables redundancy, we can help a bit to find a more elegant solution
# *** comment lines or change inital conditions if you want to play with matching
sase1.qf_2177_t2.k1 = -0.2227
sase1.qf_2192_t2.k1 = 0.211
sase1.qf_2207_t2.k1 = -0.2176
sase1.qf_2218_t2.k1 = 0.2392
sase1.qa_2229_t2.k1 = -0.9728
sase1.qa_2235_t2.k1 = 1.3215
# *** comment lines or change inital conditions if you want to play with matching
lat.update_transfer_maps()

res = match(lat, constr=constr, vars=vars, tw=sase1.tws, max_iter=2000, verbose=False)

sase1.qa_2241_sa1.k1 = kd
sase1.qa_2247_sa1.k1 = kf
sase1.qa_2247_sa1_h.k1 = kf
lat.update_transfer_maps()
tws = twiss(lat, tws0=sase1.tws)
plot_opt_func(lat, tws, legend=False)
plt.show()

    Estimation: beta_x =  4.852 ; beta_y =  20.315 ; phi =  76.0 grad; kf/kd =  1.7718 / -1.7718
    initial value: x =  [1.771751963648942, -1.771751963648942]
    Optimization terminated successfully.
             Current function value: 0.000035
             Iterations: 33
             Function evaluations: 66
    Correction: beta_x =  4.852 beta_y =  20.315  kf/kd =  1.7811 / -1.7755
    initial value: x =  [-0.2227, 0.211, -0.2176, 0.2392, -0.9728, 1.3215]
    Optimization terminated successfully.
             Current function value: 0.000001
             Iterations: 154
             Function evaluations: 275

Checking quads limits

# check quads limits
for q, k in zip(vars, res):
    print(q.id + ".k1 = "+ str(np.round(k,4)) +  ";   strength is OK :",
          quad_limits[q][0]<k<quad_limits[q][1])

    QF.2177.T2.k1 = -0.2226;   strength is OK : True
    QF.2192.T2.k1 = 0.211;   strength is OK : True
    QF.2207.T2.k1 = -0.2176;   strength is OK : True
    QF.2218.T2.k1 = 0.2393;   strength is OK : True
    QA.2229.T2.k1 = -0.9747;   strength is OK : True
    QA.2235.T2.k1 = 1.3232;   strength is OK : True