*This notebook was created by Sergey Tomin (sergey.tomin@desy.de). July 2019.

9. Accelerator based THz source

In this tutorial we will focus on another feature of the SR module (see PFS tutorial N1. Synchrotron radiation module), namely the calculation of coherent radiation. Details and limitation of the SR module in that mode can be found in G. Geloni, T. Tanikawa and S. Tomin, Dynamical effects on superradiant THz emission from an undulator. J. Synchrotron Rad. (2019). 26, 737-749

As a first step we consider a simple accelerator with the electron beam formation system (bunch compressor). Undulator parameters are chosen to generate radiation in THz range.

Accelerator
Coherent radiation from the beam

Accelerator

Accelerator includes an accelerator module and linearizer (third harmonic cavity) and a bunch compressor. IN other words we reproduce simplified version of the XFEL injector without the injector dogleg.

Lattice

# To activate interactive matplolib in notebook
# %matplotlib notebook

from ocelot import * 
from ocelot.gui import *
import time

    initializing ocelot...

#Initial Twiss parameters
tws0 = Twiss()
tws0.beta_x = 29.171
tws0.beta_y = 29.171
tws0.alpha_x = 10.955
tws0.alpha_y = 10.955
tws0.gamma_x = 4.148367385417024
tws0.gamma_y = 4.148367385417024
tws0.E = 0.005

# Drifts
D0 = Drift(l=3.52)
D1 = Drift(l=0.3459)
D2 = Drift(l=0.2043)
D3 = Drift(l=0.85)
D4 = Drift(l=0.202)
D5 = Drift(l=0.262)
D6 = Drift(l=2.9)
D8 = Drift(l=1.8)
D9 = Drift(l=0.9)
D11 = Drift(l=1.31)
D12 = Drift(l=0.81)
D13 = Drift(l=0.50)
D14 = Drift(l=1.0)
D15 = Drift(l=1.5)
D18 = Drift(l=0.97)
D19 = Drift(l=2.3)
D20 = Drift(l=2.45)


# Quadrupoles
q1 = Quadrupole(l=0.3, k1=-1.537886, eid='Q1')
q2 = Quadrupole(l=0.3, k1=1.435078, eid='Q2')
q3 = Quadrupole(l=0.2, k1=1.637, eid='Q3')
q4 = Quadrupole(l=0.2, k1=-2.60970, eid='Q4')
q5 = Quadrupole(l=0.2, k1=3.4320, eid='Q5')
q6 = Quadrupole(l=0.2, k1=-1.9635, eid='Q6')
q7 = Quadrupole(l=0.2, k1=-0.7968, eid='Q7')
q8 = Quadrupole(l=0.2, k1=2.7285, eid='Q8')
q9 = Quadrupole(l=0.2, k1=-3.4773, eid='Q9')
q10 = Quadrupole(l=0.2, k1=0.780, eid='Q10')
q11 = Quadrupole(l=0.2, k1=-1.631, eid='Q11')
q12 = Quadrupole(l=0.2, k1=1.762, eid='Q12')
q13 = Quadrupole(l=0.2, k1=-1.8, eid='Q13')
q14 = Quadrupole(l=0.2, k1=1.8, eid='Q14')
q15 = Quadrupole(l=0.2, k1=-1.8, eid='Q15')


# SBends
b1 = SBend(l=0.501471120927, angle=0.1327297047, e2=0.132729705, tilt=1.570796327, eid='B1')
b2 = SBend(l=0.501471120927, angle=-0.1327297047, e1=-0.132729705, tilt=1.570796327, eid='B2')
b3 = SBend(l=0.501471120927, angle=-0.1327297047, e2=-0.132729705, tilt=1.570796327, eid='B3')
b4 = SBend(l=0.501471120927, angle=0.1327297047, e1=0.132729705, tilt=1.570796327, eid='B4')

# Cavitys
c1 = Cavity(l=1.0377, v=0.01815975, freq=1300000000.0, eid='C1')
c3 = Cavity(l=0.346, v=0.0024999884, phi=180.0, freq=3900000000.0, eid='C3')


und = Undulator(lperiod=0.2, nperiods=20, Kx=30)
start_und = Marker()
end = Marker()
# Lattice 
cell = (D0, c1, D1, c1, D1, c1, D1, c1, D1, c1, D1, c1, D1, c1, D1, c1, D2, q1, D3,
        q2, D4, c3, D5, c3, D5, c3, D5, c3, D5, c3, D5, c3, D5, c3, D5, c3, D6, q3, D6,
        q4, D8, q5, D9, q6, D9, q7, D11, q8, D12, q9, D13, b1, D14, b2, D15, b3, D14, b4, D13,
        q10, D9, q11, D18, q12, D19, q13, D19, q14, D19, q15, D20, start_und, und, D14, end)

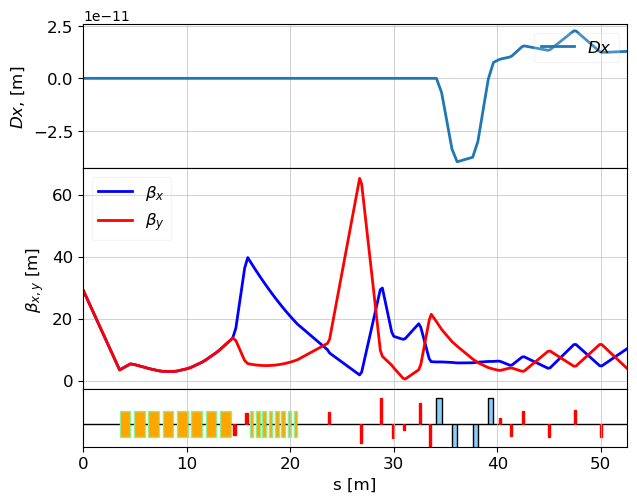
lat = MagneticLattice(cell, stop=start_und)

tws = twiss(lat, tws0)
plot_opt_func(lat, tws, legend=False, fig_name=100)
plt.show()

png

Also we can found the main parameters of the chicane with chicane_RTU(yoke_len, dip_dist, r, type)

from ocelot.utils import *
R56, T566, U5666, Sref = chicane_RTU(yoke_len=0.5, dip_dist=D14.l * np.cos(b1.angle), r=b1.l/b1.angle, type="c")
print("bunch compressor R56 = ", R56, " m")

    bunch compressor R56 =  -0.04751528087514777  m

Simple compression scenario

We consider here a basic compression scheme consisting of an accelerating module, a third-harmonic linearizer, and a magnetic chicane. For a comprehensive overview of bunch-compression physics, the following references are highly recommended:

Linear Compression with a Chicane

To compress a bunch longitudinally, the tail must have a shorter time of flight through some beamline section than the head. A standard technique is first to introduce a correlation between a particle’s longitudinal position and its energy using RF acceleration.

At the exit of a linac that induces a linear energy chirp

\delta' = \frac{1}{E_0}\frac{dE}{ds},

the mapping of the longitudinal coordinate $s$ and the relative energy deviation $\delta$ is

\begin{aligned} s_1 &= s_0,\\ \delta_1 &= \delta' s_0 + \delta_{i}, \end{aligned}

where $\delta_i = \Delta E_i / E_0$ denotes the uncorrelated energy spread.

Passing this beam through a magnetic chicane with longitudinal dispersion $R_{56}$ , the transformation (to first order) becomes

\begin{aligned} s_2 &= s_1 - R_{56}\,\delta_1 = (1 - \delta' R_{56})\, s_0 + R_{56}\,\delta_i,\\[2pt] \delta_2 &= \delta_1. \end{aligned}

Assuming $\langle s_0 \delta_i \rangle = 0$ , the rms bunch length after the chicane is

\sigma_{s_2} = \sqrt{ (1 - \delta' R_{56})^2\, \sigma_{s_0}^2 + R_{56}^2 \sigma_{\delta_i}^2 }.

The compression factor is

C = \frac{\sigma_{s_0}}{\sigma_{s_2}}.

Assuming negligible uncorrelated energy spread and choosing
$\delta' = -10$ and $R_{56} = -0.048~\mathrm{m}$ , the compression factor becomes

C = \frac{1}{1 - \delta' R_{56}} = 1.9.

Linearization with a Third-Harmonic RF System

Nonlinearities from the RF fields and from the magnetic chicane introduce curvature in the longitudinal phase space, degrading compression.
A higher-harmonic RF module can be used to compensate these nonlinearities and linearize the phase space. For the fundamental RF and its $n$ -th harmonic (with $n=3$ at the European XFEL), the normalized RF amplitudes must satisfy

\begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & -k & 0 & -n k \\ -k^2 & 0 & -(nk)^2 & 0 \\ 0 & k^3 & 0 & (nk)^3 \end{bmatrix} \begin{bmatrix} V_1 \cos\phi_1 \\ V_1 \sin\phi_1 \\ V_{13} \cos\phi_{13} \\ V_{13} \sin\phi_{13} \end{bmatrix} = \frac{1}{e} \begin{bmatrix} E_1 - E_0 \\ E_1\delta_2' - E_0\delta_0' \\ E_1\delta_2'' - E_0\delta_0'' \\ E_1\delta_2''' - E_0\delta_0''' \end{bmatrix}.

We assume initial conditions:

E_0 = 5~\mathrm{MeV}, \qquad \delta_0' = \delta_0'' = \delta_0''' = 0.

As a target after the RF system (and before the chicane), we choose:

E_1 = 130~\mathrm{MeV}, \qquad \delta_2' = -10, \qquad \delta_2'' = \delta_2''' = 0.

Thus, the right-hand side becomes

\begin{bmatrix} 125 \\ -1300 \\ 0 \\ 0 \end{bmatrix}.

Additional Contribution from the Undulator

Note:
The earlier estimate of $R_{56}$ included only the chicane.
The undulator also contributes to longitudinal dispersion.

For an undulator with large $K$ -value, the longitudinal dispersion is

R_{56} = -\frac{L_u}{\gamma}\left( 1 + \frac{K^2}{2} \right) \approx -0.028~\mathrm{m}.

Including this contribution, the total compression factor becomes

C = \frac{1}{1 - \delta R_{56}} = 4.1.

import scipy.optimize

# M*a = b
k = 2*np.pi/3e8*1.3e9
n = 3 
M = np.array([[1,     0,      1,          0],
             [0,      -k,     0,       -(n*k)],
             [-k**2,  0,   -(n*k)**2,     0],
             [0,      k**3,   0,      (n*k)**3]])


b = np.array([125, -1300, 0, 0])
def F(x):
    V1 = x[0]
    phi1 = x[1]
    V13 = x[2]
    phi3 = x[3]
    V = np.array([V1*np.cos(phi1*np.pi/180),
             V1*np.sin(phi1*np.pi/180),
             V13*np.cos(phi3*np.pi/180),
             V13*np.sin(phi3*np.pi/180)]).T
    return np.dot(M, V) - b

x = scipy.optimize.broyden1(F, [150, 10, 20, 190])
V1, phi1, V13, phi13 = x
print("V1 = ", V1, " MeV")
print("phi1 = ", phi1)
print("V13 = ", V13, " MeV")
print("phi13 = ", phi13)

    V1 =  150.53461560292047  MeV
    phi1 =  20.905449650430196
    V13 =  15.751142632839656  MeV
    phi13 =  187.25608275658084

Now we update cavities parameters in the lattice

# type new parameters, 
# NOTE in OCELOT cavity voltage in [GeV] so to traslate calculated voltage we need factor 1/1000 
# and we have 8 cavities for main RF module and linearizer 
c1.v = V1/8/1000
c1.phi = phi1
c3.v = V13/8/1000
c3.phi = phi13

# and update lattice 
lat.update_transfer_maps()

    <ocelot.cpbd.magnetic_lattice.MagneticLattice at 0x168570ac0>

Generate electron beam

np.random.seed(10)
parray = generate_parray(sigma_x=0.0001, sigma_px=2e-05, sigma_y=None, sigma_py=None, 
                         sigma_tau=0.001, sigma_p=0.0001, chirp=0.0, charge=0.5e-09, 
                         nparticles=300, energy=0.005, tau_trunc=None)

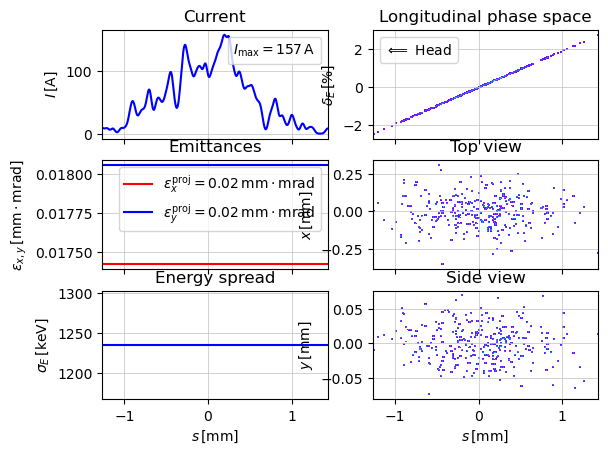
show_e_beam(parray,nparts_in_slice=50,smooth_param=0.1, nbins_x=50, nbins_y=50, nfig=10)
plt.show()

png

Tracking up to undulator

navi = Navigator(lat)
tws_track, parray = track(lat, parray, navi)
show_e_beam(parray, nfig=201)
plt.show()

    z = 52.547084483708005 / 52.54708448370802. Applied: 

png

parray.E

    0.13000000268915646

Coherent radiation from the beam

from ocelot.rad import *
lat = MagneticLattice(cell, start=start_und, stop=end)

screen = Screen()
screen.z = 1000.0
screen.size_x = 15
screen.size_y = 15
screen.nx = 1
screen.ny = 1
screen.start_energy = 0.001  # eV
screen.end_energy = 3e-3  # eV
screen.num_energy = 1001

# to estimate radiation properties we need to create beam class 

beam = Beam()
beam.E = 0.13

# NOTE: this function just estimate spontanious emmision
print_rad_props(beam, K=und.Kx, lu=und.lperiod, L=und.l, distance=screen.z)

    ********* ph beam ***********
    Ebeam        :  0.13  GeV
    K            :  30
    B            :  1.6065  T
    lambda       :  6.96835E-04  m 
    Eph          :  1.77925E-03  eV
    1/gamma      :  3930.7605  um
    sigma_r      :  5941.5531  um
    sigma_r'     :  9332.9698  urad
    Sigma_x      :  5941.5531  um
    Sigma_y      :  5941.5531  um
    Sigma_x'     :  9332.9698 urad
    Sigma_y'     :  9332.9698 urad
    H. spot size :  9332.9717 / 9.333  mm/mrad
    V. spot size :  9332.9717 / 9.333  mm/mrad
    I            :  0.0  A
    Nperiods     :  20.0
    distance     :  1000.0  m
    flux tot     :  0.00E+00  ph/sec/0.1%BW
    flux density :  0.00E+00  ph/sec/mrad^2/0.1%BW;    0.00E+00  ph/sec/mm^2/0.1%BW
    brilliance   :  0.00E+00  ph/sec/mrad^2/mm^2/0.1%BW

start = time.time()
screen_i = coherent_radiation(lat, screen, parray, accuracy=1)
print()
print("time exec: ", time.time() - start, " s")
show_flux(screen_i, unit="mm", title="")

    n: 299 / 299
    time exec:  100.35891485214233  s

png

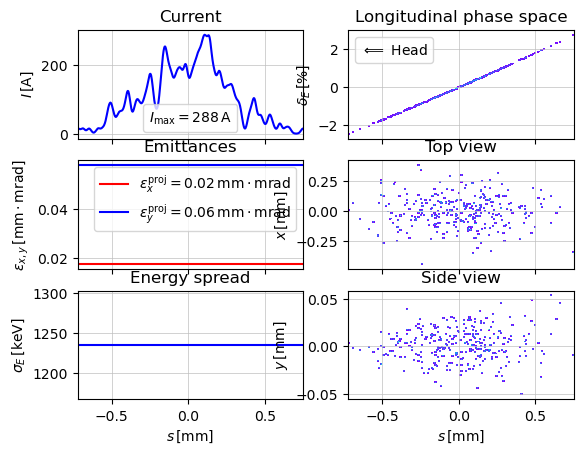
Beam after undulator.

as you can notice, the beam was compressed in the undulator in approximatly in two times as was calculated in the Simple compression scenario

show_e_beam(parray,  nfig=203)
plt.show()

png

Electron trajectories

In some cases, it is worth checking the trajectory of the particle used to calculate the radiation. For this purpose, a special object BeamTraject is attached to the object screen after radiation calculation:

screen.beam_traj = BeamTraject()

To retrieve trajectory you need to specify number of electron what you are interested, for example:

x = screen.beam_traj.x(n=0)

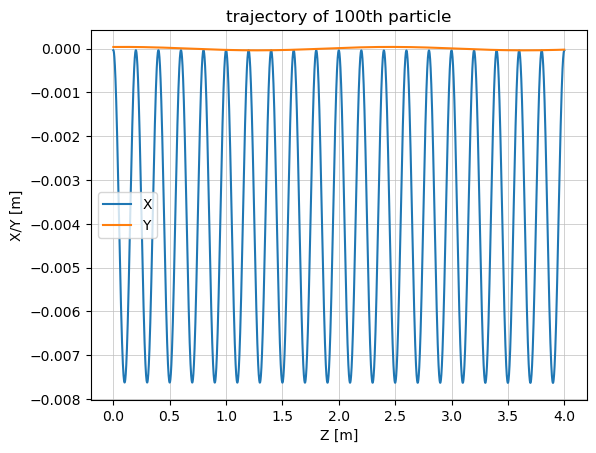
n = 100
x = screen.beam_traj.x(n)
y = screen.beam_traj.y(n)
z = screen.beam_traj.z(n)
plt.title("trajectory of " + str(n)+"th particle")
plt.plot(z, x, label="X")
plt.plot(z, y, label="Y")
plt.xlabel("Z [m]")
plt.ylabel("X/Y [m]")
plt.legend()
plt.show()

png

Contents​

Accelerator​

Lattice​

Simple compression scenario​

Linear Compression with a Chicane​

Linearization with a Third-Harmonic RF System​

Additional Contribution from the Undulator​

Generate electron beam​

Tracking up to undulator​

Coherent radiation from the beam​

Beam after undulator.​

Electron trajectories​

Contents